Cartesian tree or treap (binary search tree + binary heap) is a fast yet simple data structure. It conforms to a core search binary tree property and binary heap property at the same time. Despite its simplicity, treap self-balances, resulting in O(logn) complexity on average for all common operations.
Amazing, right?
O(logn) complexity is on average. However, with a lot of items O(logn) is almost always true. So, later in this article, I will use just O(logn) without "on average" addition.Moreover, there is a modification (implicit treap, treap with implicit key) that lets you use treap as a usual array with O(logn) random insertions and random deletions. Isn't it cool? In this article I'll explain how to create one and provide the implementation in Swift. Also, I will compare treap to the general set from standard library. Let's start!
Core algorithm
As I said earlier, treap combines heaps and binary search trees. Therefore, we are going to store at least two properties: key (or value) and priority. Key is a value for which tree is a search tree and for the priority, it is a binary heap.
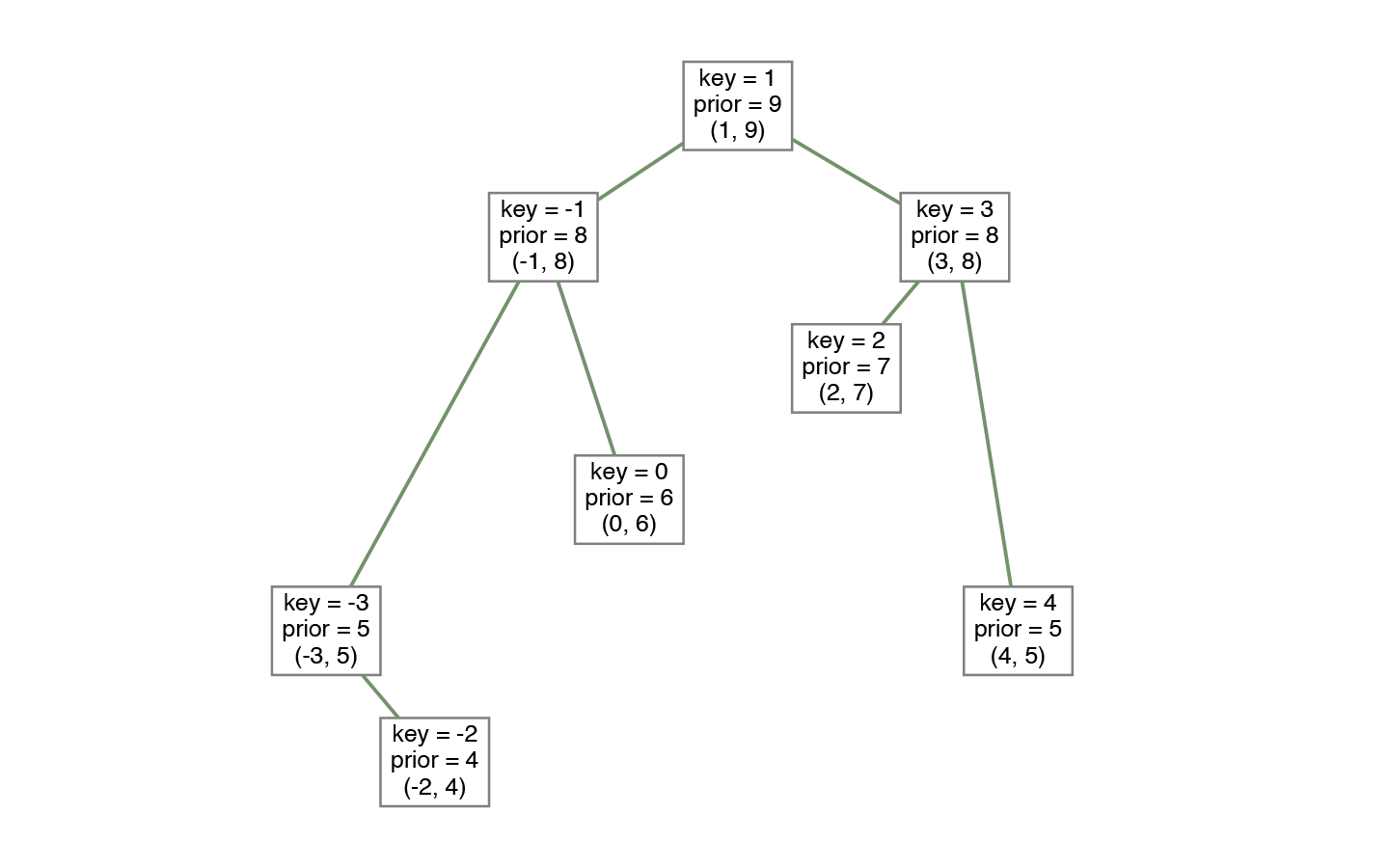
On the image above, you may notice that for every node, all child's priorities are less. On the other side, all children on the left have a key less than that in the node, and all children on the right have a larger key.
To create a fully-functioning search tree, we need to implement:
- find
- insert
- remove
More exotic operations like lower bound and upper bound are also pretty simple and does not differ from those in the other search trees. And all these operations can be implemented using just two helper operations!
How to do that?
Splits the tree into two trees by given
value. All values in the left tree are less than the value while in the right tree are greater. And both resulting trees are correct treaps. We will use a special flag that decides whether to send values that are equal to the left tree or to the right tree.
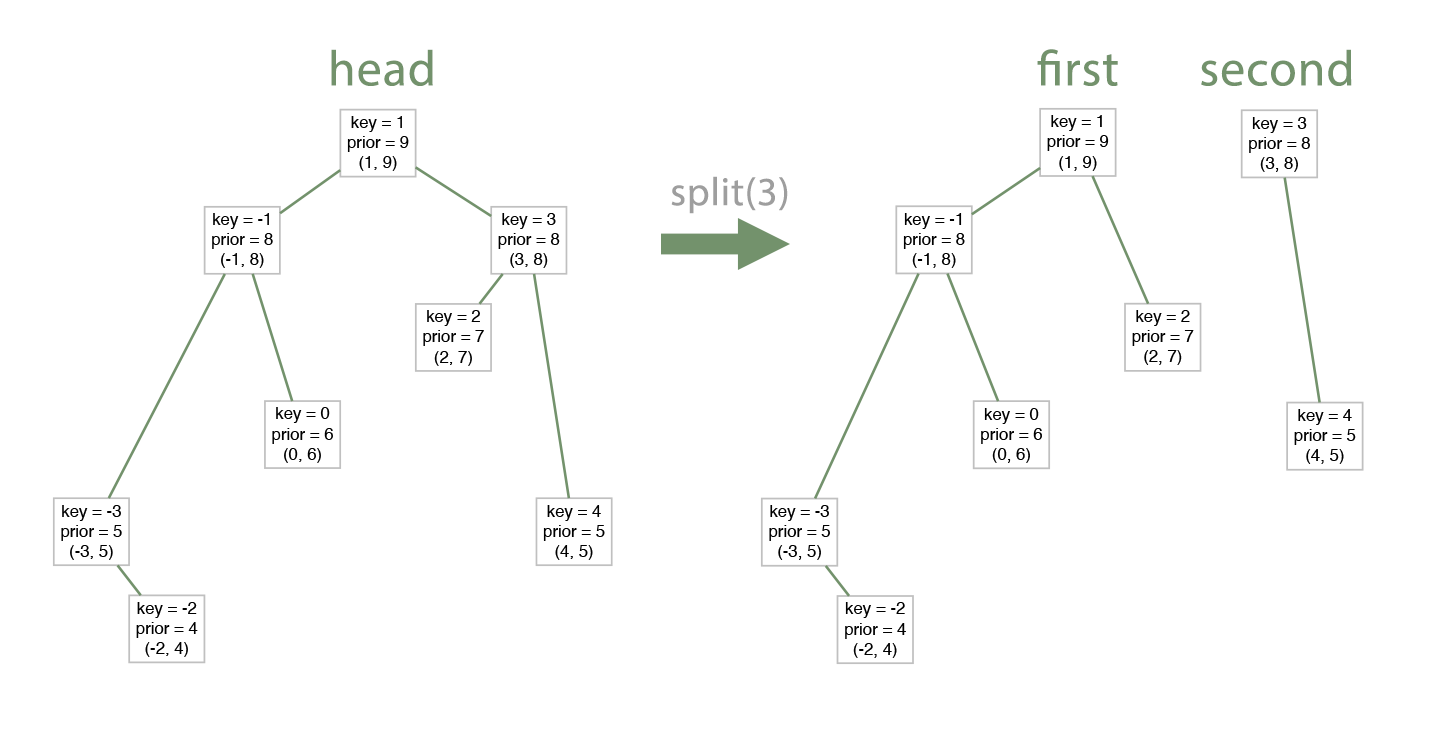
Merges two treaps into one big treap.
Prerequisite: all items in the first tree are less than items in the right tree.
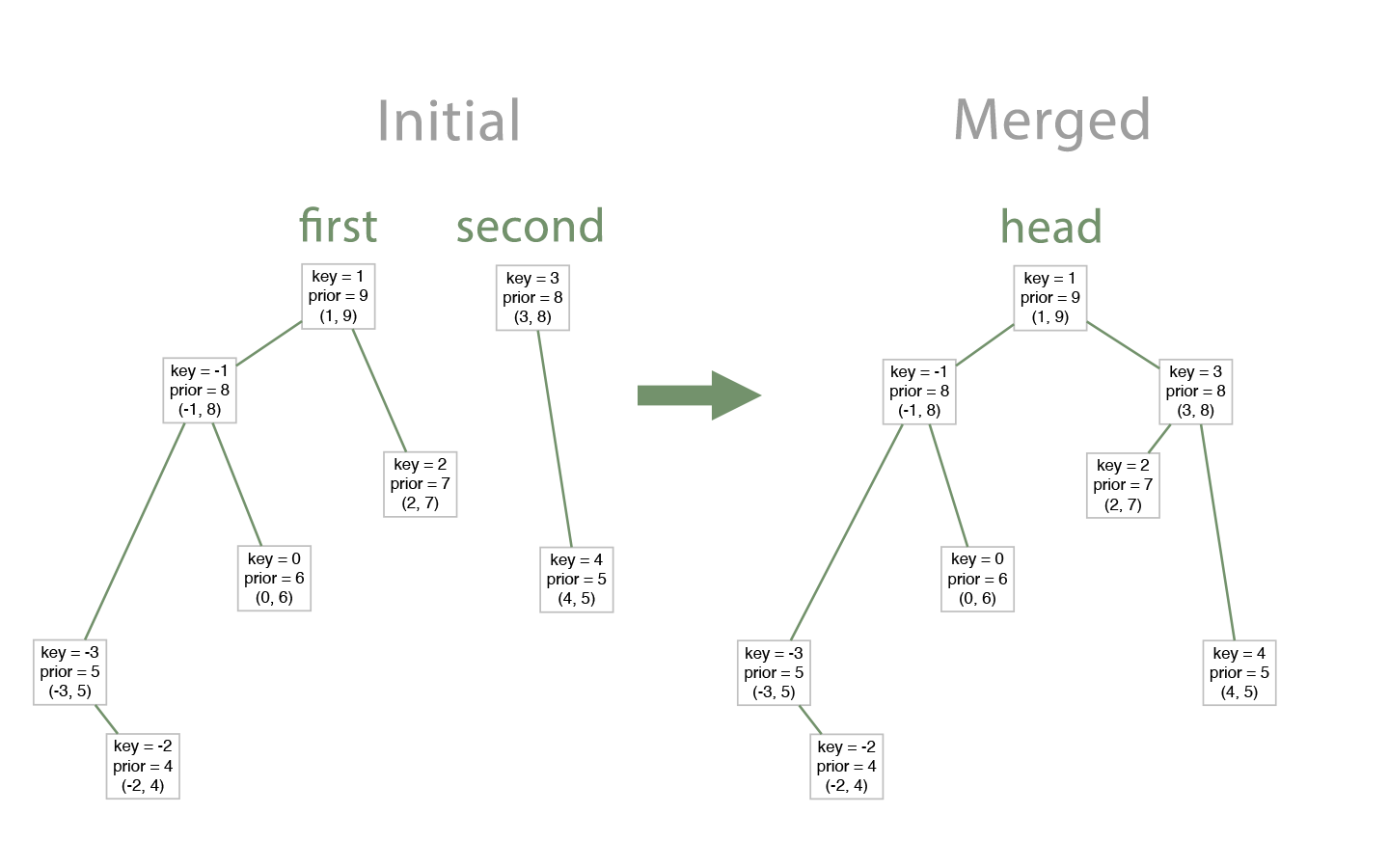
So, if we implement these two methods, implementing all other three operations would be trivial.
Split
Let's start thinking about code at this stage. I'm going to explain this in C++. Rewriting the following code in Swift is actually really easy. Leave a comment bellow if you need a help.
template<typename T>
struct Node {
T key;
size_t prior;
Node* left = nullptr, *right = nullptr;
Node(T key, size_t prior) :
key(std::move(key)),
prior(prior) {
}
};For split, we have a head node and a key for which split needs to be done. This method is extremely simple using recursion.
Algorithm
Let the current head be p.
- If
p->keyis less than thekey, then we need to go right and splitp->rightfurther.
Also, splittingrightwill bring two trees as well, and the first one will have nodes with keys less than thekey. Yet, they are greater than thep->key(as they are in the second tree of the first split).
So, we setp->rightto the first tree of splittingrightresult.
Result:p, split right's second tree - If the
p->keyis greater or equal to thekey, then we need to go left and splitp->leftfurther.
Similarly to the case above, we setp->leftto the second tree of split left.
Result: split left's first tree,p
The algorithm above leaves a node that is equal to the split value in the second tree. Symmetrically, we will use the equalOnTheLeft flag to leave the node in the left tree.
So, the final code:
pair<Node *, Node *> split (Node *p, const T& key,
bool equalOnTheLeft=false) {
if (!p) // reached leaf
return {nullptr, nullptr};
if (p->key < key ||
(equalOnTheLeft && p->key == key)) { // splitting right
auto q = split(p->right, key, equalOnTheLeft);
// q.first has nodes of the right
// subtree that are less than key
p->right = q.first;
return {p, q.second};
} else { // splitting left
auto q = split(p->left, key, equalOnTheLeft);
// q.second has nodes of the left
// subtree that are greater or equal
// to the key
p->left = q.second;
return {q.first, p};
}
}Merge
Merge is similar to split, but it uses priorities to do the work. As I mentioned before, there is a prerequisite: all items in the first merged tree must be less than items in the second tree. If this is not true, another algorithm must be used.
Algorithm
Similarly to split, merge is also recursive. Let us have two trees to merge: l and r.
- We need to choose which tree will represent the new head. That's simple — the head must have the greatest priority, so we choose
lorrbased on that.
l has the highest priority in the whole l tree as its a property of correct treap. The same applies to r.- If
lhas greater priority, thenl->leftsubtree will remain intact as left subtree for sure less thanrand it has nothing to do with it.
Then,l->rightsubtree must be merged withrand it's going to be the newl->rightsubtree. - If
rhas greater priority, then, similar to the example above,r->rightwill remain intact andr->leftmust be merged withl
Node* merge (Node *l, Node *r) {
if (!l) // left is empty
return r;
if (!r) // right is empty
return l;
if (l->prior > r->prior) { // l has the new head.
l->right = merge(l->right, r);
return l;
} else { // r has the new head.
r->left = merge(l, r->left);
return r;
}
}Why is it correct?
It seems like nothing stops us from breaking the search tree structure where all items' values in the left subtree are less than the node's value, and all items in the right subtree are greater.
l < r property is always kept the sameImplementing search tree methods
You believed me that all methods are easy to implement through split and merge. Time to prove that.
Find
Find is implemented just like for the general search tree. We use the fact that keys in the left subtree are greater than the value in the node.
Node* find(Node* node, const T& key) {
if (node == nullptr)
return nullptr;
if (node->key == key)
return node;
return find(key >= node->key ? node->right : node->left, key);
}Insert
Let's think about insert in terms of split and merge. We have one big tree and we need to insert a new key.
- Split the tree by
keyto new trees:firstandsecond. Then, we will have two trees: the first (which has values lower than thekey) and the second (which has values greater or equal to thekey).
We can check that node already exists: try to find it in the right tree.
If you need to insert multiple copies of the same item, you can store an item and it's count to achieve that
- Create a new node that will store the new
key—newNode. Ta-da this node is a correct treap that has only one node.
For the new node, you need to set a random priority
O(logn) complexity for all operations- New head will be
merge(first, merge(newNode, second))
See? It's that simple.
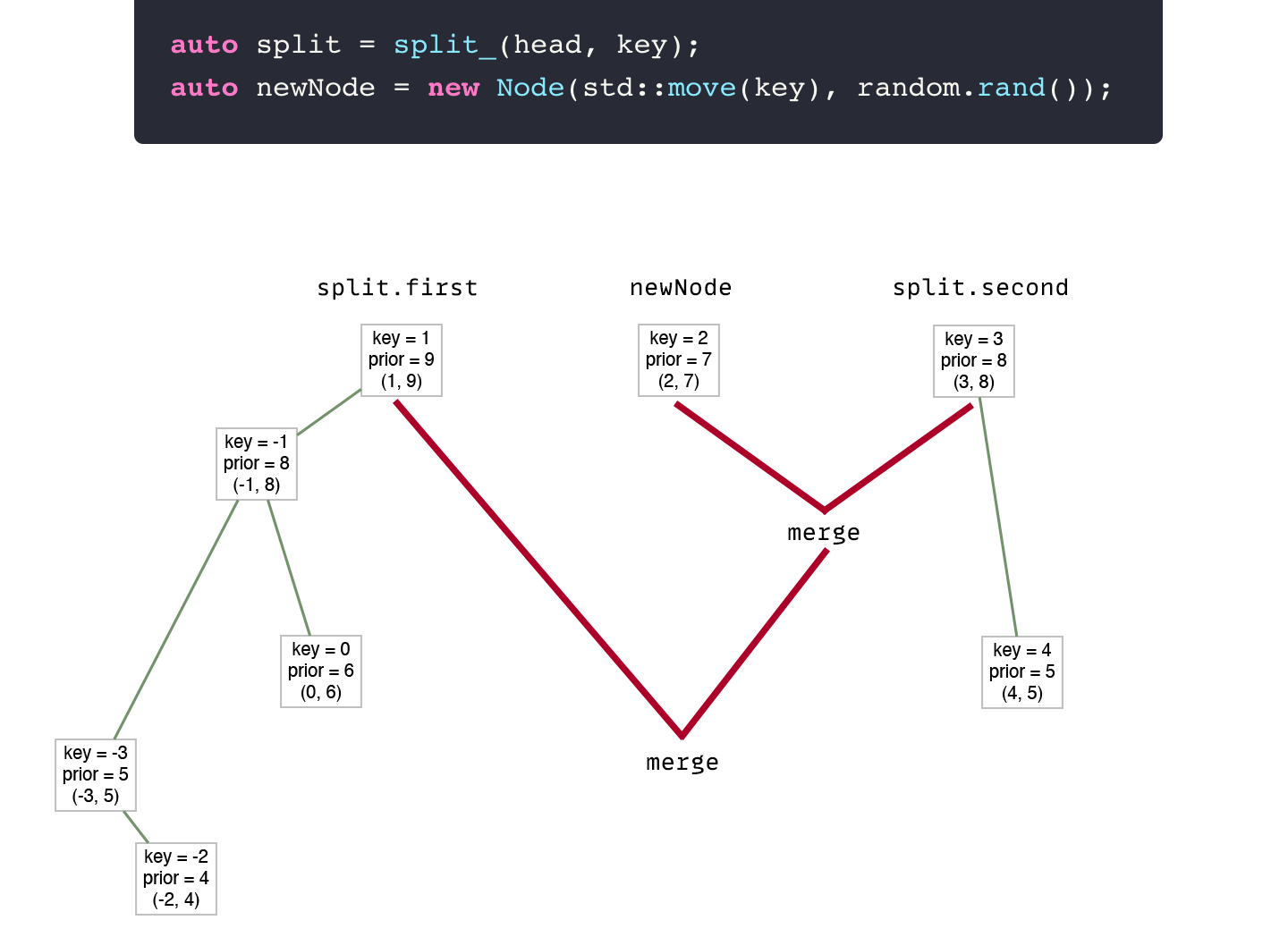
Node* insert(Node* head, T key) {
auto split = split(head, key);
if (find(split.second, key) != nullptr) {
// Key exists already
// Merge back
return merge(split.first, split.second);
}
auto newNode = new Node(std::move(key), rand());
return merge(split.first, merge(newNode, splitsplitted.second));
}Remove
It's very similar to insert. However, that's where the equalOnTheLeft flag is used.
second tree produced by split contains items greater or equal to the selected keyTherefore, the second tree will contain the value that needs to be removed. But how to remove it from the tree?
Split again.
We can split the second tree by key, setting the equalOnTheLeft flag to true. Thus, the node will be separated from the second tree to the new tree.
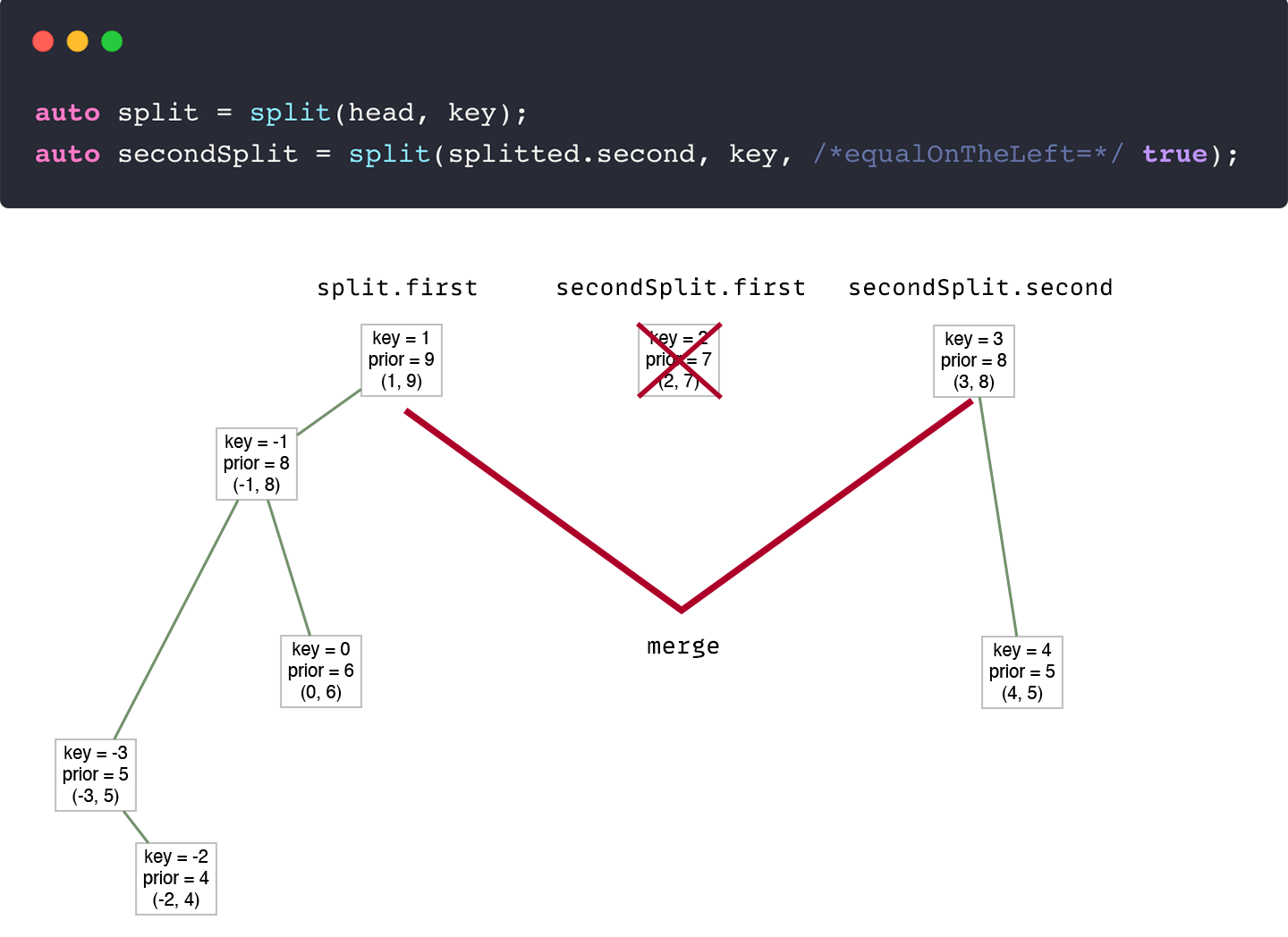
Node *remove(Node *head, const T &key) {
auto split = split(head, key);
if (split.second) {
auto secondSplit = split(split.second, key,
/*equalOnTheLeft=*/true);
// Key exists, so delete it and merge
auto everythingElse = secondSplit.second;
if (secondSplit.first == nullptr) {
// There's no element equal to key. Merge back.
return merge(split.first, everythingElse);
}
// We got node with key value in
// secondSplit.first
delete secondSplit.first;
size--;
return merge(split.first, everythingElse);
}
// Key is not presented. Merge back.
return merge(split.first, split.second);
}Full code
You can download C++ code of a little bit optimized Treap here:
Comparing to std::set
First of all, the implemented version of treap utilizes split and merge methods. Note that there is more efficient implementation that uses rotations. However, the true power of treap is in split and merge methods as other search trees can't do it easily.
Find tests

It's visible that asymptotics is similar. Though, treap always has the greater overhead. Still, it's a good result! We're competing with an utterly optimized standard library data structure.
Inserts

Insertion has even bigger overhead. And it was expected: recursive calls of merge and split do not improve performance ;)
Comparison conclusion

As you see, treap has higher nodes' height on average than that of very well-balanced AVL tree.
Yes, treap has worse performance than that of std::set. Yet, the results are comparable, and with a large data size, treap gets closer and closer to std::set which in fact is a red and black tree.
Believe me, you don't want to write your own RB tree. It's a nightmare.
Use cases and modifications
We developed this data structure not just to lose std::set. There are several useful applications.
Sum of numbers in the interval
We need to modify Node structure, adding sum field. It will store sum of all its children and itself.
template<typename T>
struct Node {
T key;
size_t prior;
long long sum;
Node* left = nullptr, *right = nullptr;
Node(T key, size_t prior) :
key(std::move(key)),
prior(prior) {
}
};It's extremely easy to update the sum. Every time childs are changed, sum = left->sum + right->sum. So, you can implement some kind of update function and call it in split and merge right before returning value. That's it.
How to answer on request?
We receive interval [l, r]. To calculate the sum of numbers on this interval, we can split the tree by l, then split the second tree of the result by r+1 (or by r, leaving equal elements on the left). In the end, we will have a tree containing all added numbers in the interval [l, r].
Complexity: O(logn) versus O(n) naive.
Using a hash of value in place of priority
You can use a hash of value as a priority as a good hash function is pretty random. What benefits does it bring?
If keys and priorities are fixed, then no matter how you construct the treap or add elements, it's always going to have the same structure.
Therefore, you can compare two sets in O(n) as treaps containing the same values will have absolutely the same structure.
Implicit treap
What if we use the size of the left subtree as a key? Then, we can use this key as an index. Wow. That means that we can represent a regular ordered array as a treap!
By doing this, we can:
- make insertions by random index
O(logn)versusO(n)naive - make deletions by random index
O(logn)versusO(n)naive
With great power, comes great responsibility.
O(logn) versus O(1) in the standard array.If your algorithm requires a lot of array modifications and very few accesses/outputs, then it's the right choice. Moreover, you can convert treap into an array and back with O(n) complexity.
Cut-paste problem
Imagine that you have a big string and you recieve requests to cut some part and to insert it somwhere.
This problem can be solved using treaps with implicit key. You can use splits to cut needed part and merge to insert it.
FAQ
Cartesian trees are most suitable for what?
Treap is useful when you need to collect some kind of characteristic on an interval (for example, sum) or apply some modification to the interval. Treap with implicit key is also useful when you need to apply a lot of random tree insertions/deletions with few accesses.
Why don't we use array indices as keys for an implicit treap?
Because in case of insertion we would need to recalculate all indeces that are higher than inserted index. Therefore, it downgrades complexity to O(n).
Is treap a randomized tree?
Yes, it is. But it can also use hash value in place of a random value.
I know about implementation without split and merge. It utilizes left and right turns. Is it better?
For example, GeeksforGeeks use such implementation, I know. But I believe that the true value of treap is in seampless splits and merges. You've already seen by examples how it is really usefull. Why implementing treap with turns when you can build AVL that's probably going to be faster?
Love data structures?
Check out my article on the amazing Skip List! While a lot of people never heard about it, Skip List is beautiful and can solve, for example, the problem of finding the n-th maximum or the rolling median problem in the most efficient way.
Also, you can check the whole algorithms section of my blog

References

https://www.cs.cmu.edu/~scandal/papers/treaps-spaa98.pdf