Skip List is a nice structure that lets you to perform O(logn) insertions into sorted list, O(logn) searches and O(logn) for finding n-th — second, third, fourth, ... — maximum or even calculating the rolling median. In this article I focus on indexation of skip list (indexable skip list).
The best guide I found was “a skip list cookbook” last revised in 1990. It slightly touched the problem of finding the kth element, but the provided algorithm is extremely vague and refers to unknown quantities without giving the information on how to find these quantities or update (ex. fDistance[i]). Wikipedia also talks about indexing, but an algorithm for calculating skip distances is not provided.

Therefore, I decided to create this post and provide an algorithm for indexing skip lists. Here, I’m going to give the code as well.
About skip list
A skip list is a one-way linked list that has “express lanes” for reaching distant members. It is a probabilistic data structure: selecting the "height" of each node relies on random numbers. As a result, it provides O(logn) insert and search complexity.
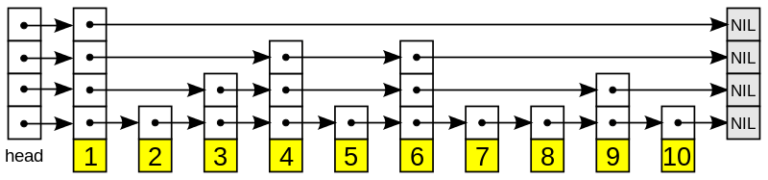
O(n) to O(logn)Each node has a link to the right node on the same level and a link to the bottom node that has the same value, but one level lower. The first layer doesn’t have a bottom link. Some nodes don’t have the right node. We consider the null right node as \(+\infty\) and head as \(-\infty\).
To search for an element, we start at the left top corner and move: right if the right element is lower or equals to the needed element or move down if it is bigger than the required element.
Indexing skip list allows us to calculate the rolling median of set in O(logn) and to find n-th minimum or maximum in O(logn) also!
Defining the node
Each node is going to be:
template<typename T>
struct TreeNode {
T key;
unsigned level = 1;
bool headNode = false;
bool deleted = false;
size_t skipDist = 0;
TreeNode<T>* right = null;
TreeNode<T>* down = null;
}key– stored valuelevel– the level of the nodeheadNode– is this node is the head nodedeleted– the node is marked as deletedskipDist– distance skippedright– right nodedown– down node
We need to define the deleted mark as we can’t delete the node immediately due to the fact that the list is one-way linked. We just can’t update the left to the deleted one’s member. On the other hand, such a feature is useful in multi-threaded projects.
On this figure you can see what skipDist means:
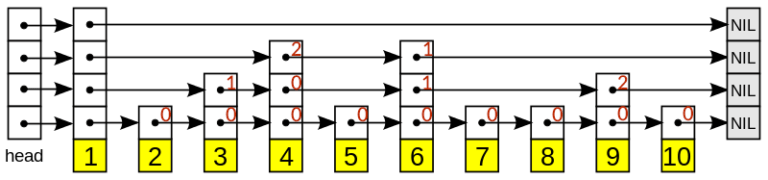
skipDist counts how many nodes will be skipped if you travel by the according fast laneDefining skip list
template<typename T>
class SkipList {
unsigned maxLevels;
TreeNode<T>* head;
}Pretty much self-explanatory structure.
On initialisation, we create maxLevels number of head nodes:
this->head = new TreeNode<T>(0, this->maxLevels);
this->head->headNode = true;
TreeNode<T>* pos = this->head;
for(unsigned i = 1; i < maxLevels; ++i) {
TreeNode<T>* newNode = new TreeNode<T>(0, this->maxLevels - i);
newNode->headNode = true;
pos->down = newNode;
pos = newNode;
}Insert
The hardest part of the insert algorithm is to update skip distances and to create upper-level nodes if random coin said so.
As I discussed previously, we do not delete elements, but rather mark them as deleted. therefore, before processing, we need to perform deletions. Let it be some function processDeletions(node). It finally deletes the element right to the node if it was marked as deleted.
Also, to check for cases when the right node is null, I created a function that compares node value to the key value.
// key < node
int compareWithNode(T key, TreeNode<T>* node){
if (node == nullptr)
return -1;
if (key == node->key)
return 0;
return key < node->key ? -1 : 1;
}compareWithNode returns 0 if values are equal, -1 if the key is lower than the node value, and 1 if the key value is higher than the node valueAs discussed before, if we encounter a null node, then we consider it as +inf.
To perform all desired operations, the insert function is going to accept the current node, desired key, a pointer to the inserted node (if any), current position. We need to have a pointer to the inserted node for two reasons: to know on the higher levels whether the node was inserted at all, and we need the link to the bottom if we generate a “fast lane” node.
Also, let the function return bool value: whether the node was inserted on the previous level. If it was inserted, then we can flip the coin again and insert the “fast lane” node again on the current level.
bool insertRecursive(TreeNode<T>* node,
T key,
TreeNode<T>** insertedOne,
unsigned* pos) {
this->processDeletions(node);
int compareRight = compareWithNode(key, node->right);
// save position at the current recursion level
unsigned posHere = *pos;
if (compareRight == 0 ||
(node->key == key && node->headNode != true))
return false;In the case, if the right node value is equal to the desired or the current node value is equal to the desired and this node is not the head node, the function returns with false as no insertions were needed.
Finally, if the right node’s value is lower than the desired, the function just increases the pos counter for the right node’s skip distance + 1 and dives deeper.
if (compareRight == 1) { // right elem is lower
*pos += node->right->skipDist + 1;
return insertRecursive(node->right,
key,
insertedOne,
pos);
}Interesting things happen if we go down. First of all, if we need to go lower and it’s the very first level, then we simply insert the node and return true as the node was inserted.
else { // (compareRight == -1) // want go down
if (node->level == 1) {
*(insertedOne) = new TreeNode<T>(key, 1, ++(this->ids));
(*(insertedOne))->right = node->right;
node->right = *(insertedOne);
return true;
}If we can go down, then some cases are needed to be considered.

We need to go deeper. That means that on the current level the right node’s value is higher than the desired, so the insertion is going to occur before the right node. That means that the right node’s skip distance is going to be increased by 1.
Also, if on the current level we insert a fast lane node, then the right node’s skip distance is shortened by the skip distance of the inserted node.
else {
// whether there was an insertion on the deeper level
bool possibleLevelInsert = insertRecursive(node->down,
key, insertedOne, pos);
if (!possibleLevelInsert ) {
// if insertion of fast lane is impossible
if (node->right != nullptr && *insertedOne != nullptr) {
// if right node on the current level is presented
// and we inserted the node (*insertedOne != nullptr)
node->right->skipDist++;
}
return false; // insert of further fast lanes is impossible
}
At this point, we know that we can insert a fast lane node on the current level. Let’s spin a coin and decide.
if(node->level == 1) // trivial case
return true;
bool insertNow = this->spinACoin();
if (!insertNow){
// no fast lane insertion -> increase the next
// fast lane skip distance as the node was inserted somewhere between.
if (node->right != nullptr){
node->right->skipDist++;
}
return false;
}
// Can insert the fast lane node
TreeNode<T>* newNode = new TreeNode<T>(key, node->level);
newNode->down = *(insertedOne);
newNode->right = node->right;
newNode->skipDist = (*pos - posHere);
// *pos stopped updating at the insertion position.
// At the beginning, we saved temporary pos at the current recursion level.
if (node->right != nullptr) {
// shrink right node skip distance as we inserted new fast lane node
node->right->skipDist -= newNode->skipDist;
}
node->right = newNode;
*(insertedOne) = newNode;
return true;This was massive code. Final insert function:
bool insertRecursive(TreeNode<T>* node, T key, TreeNode<T>** insertedOne, unsigned* pos){
this->processDeletions(node);
int compareRight = compareWithNode(key, node->right);
unsigned posHere = *pos;
if (compareRight == 0 || (node->key == key && node->headNode != true))
return false;
if (compareRight == 1){ // right elem is lower
*pos += node->right->skipDist + 1;
return insertRecursive(node->right, key, insertedOne, pos);
} else {// (compareRight == -1) // want go down
if (node->level == 1){
*(insertedOne) = new TreeNode<T>(key, 1);
(*(insertedOne))->right = node->right;
node->right = *(insertedOne);
return true;
} else {
bool possibleLevelInsert = insertRecursive(node->down, key, insertedOne, pos);
if (!possibleLevelInsert ){
if (node->right != nullptr && *insertedOne != nullptr){
node->right->skipDist++;
}
return false;
}
if(node->level == 1)
return true;
bool insertNow = this->spinACoin();
if (!insertNow){
if (node->right != nullptr){
node->right->skipDist++;
}
return false;
}
TreeNode<T>* newNode = new TreeNode<T>(key, node->level);
newNode->down = *(insertedOne);
newNode->right = node->right;
newNode->skipDist = (*pos - posHere);
if (node->right != nullptr) {
node->right->skipDist -= newNode->skipDist;
}
node->right = newNode;
*(insertedOne) = newNode;
return true;
}
}
}Process deletions
The only thing that left is to define the processDeletions(node) function. If the right node is marked as deleted, then we need to update right to the right node skip distance. Also, at first, it’s needed to go to the deepest level of recursion and perform alterations from the end to the start.